„Ezt nem tanították meg rendesen, de az államvizsga tételekbe azért beletették...”

A fenti panasszal egy online fórumon találkoztam. A vizsgára készülő főiskolásnak a fő-, iker- és melléktermékek önköltségszámításával és számvitelével gyűlt meg a baja.


Nem tudom, az érintett azóta sikeresen túlesett-e a vizsgán vagy sem, de a fentiek bizonyára más könyvelőpalántáknak is okoztak már gondot.

Fontos kérdésről van szó, hiszen az ipari és mezőgazdasági termelő vállalkozások gyakorlatában sokszor előfordul, hogy valamely termék előállításával párhuzamosan, ugyanazon alapanyagból, ugyanazon technológiai folyamatban egy másik termék is létrejön. E termékeket az alá- és fölérendeltségi kapcsolatuk szerint minősítjük főterméknek vagy mellékterméknek.

A főtermék az a termék, amely az adott vállalkozás termelési tevékenységének fő célja, míg a melléktermék a főtermék mellett keletkezik, annak velejárója, az ikertermékek pedig azok, amelyek egyenrangú termékeknek minősülnek.

A fő- és melléktermék kapcsolatra szemléletes példa:
- növénytermelésben a búza és a szalma,
- állattenyésztésben a tej, hús, trágya, borjúszaporulat, a toll, a tojás,
- az élelmiszeriparban a liszt és a korpa,
- kőolaj-finomítás esetében a benzin, pakura, kenőolaj, stb.,
- az asztalos üzemben a bútorok és az előállításuk során keletkező faforgács.
Ikertermékek lehetnek a pékségben a kenyér és a kifli.
Önköltséget számíthatunk az összes költség alapján vagy csak a közvetlen előállítási költség alapján, attól függően, hogy az általános költségek termékre vagy szolgáltatásra eső részét szerepeltetjük-e a kalkulációban.
A fentiekben megismert termékkategóriák függvényében, az önköltségszámítás alapesetei:
- amennyiben a termelési folyamatban csak egy főterméket vagy szolgáltatást állít elő a vállalkozás, akkor a termelés összes költségét elosztva a megtermelt termék vagy szolgáltatás mennyiségével az önköltséget kapjuk, míg
- ha a termelés során fő- és melléktermék is képződik, akkor a termelés összes költségéből, azaz a bruttó költségből le kell vonni a melléktermék értékét vagy annak költségét, és az így megmaradó nettó költséget osztjuk el a megtermelt termékek vagy szolgáltatások mennyiségével, azonban akkor
- ha iker és melléktermékek egyaránt képződnek a termelés során, akkor kétféle eljárást alkalmazhatunk. Jelesül:
 arányszámos osztókalkuláció alkalmazása esetén a nettó termelési költséget előre meghatározott arányszám alapján osztjuk fel. Ez az arányszám kötődhet egy rögzített viszonyítási alap arányszámaihoz is, míg
 egyenértékszámos osztókalkuláció esetén először kiszámítjuk a nettó termelési költséget oly módon, hogy a termelés összes költségéből, azaz a bruttó költségből levonjuk a melléktermék értékét vagy annak költségét. Ezután egy átszámítási kulcs alapján egyetlen termékben – vezértermékben – fejezzük ki az összes ikerterméket. Ennek az egy terméknek meghatározzuk az önköltségét, majd az átszámítási kulcs segítségével kifejezzük a többi ikertermék önköltségét is.

Arányszámos önköltségszámítás: akkor ajánlott, amikor a főtermék mellett többféle eltérő értékű termék keletkezik. Lényege: a melléktermék értékével csökkentett termelési költséget először a termékek pénzértékének százalékos arányának megfelelően meg kell osztani. Ezt követően az egyes termékekre jutó összes költség és azok mennyiségének hányadosaként állapítható meg a társtermékek önköltsége. Ez az arányszám kötődhet egy rögzített viszonyítási alap arányszámaihoz is. (A mezőgazdaságban alkalmazható – például - a juhászatban a gyapjú, a bárány és a tej meghatározásakor.)

Nézzünk erre egy példát is a mezőgazdaságból!
Egy növénytermesztéssel foglalkozó vállalkozás alábbi számviteli adataiból a lucerna-széna és a lucernamag önköltségét (ÖK) kell kiszámítanunk.



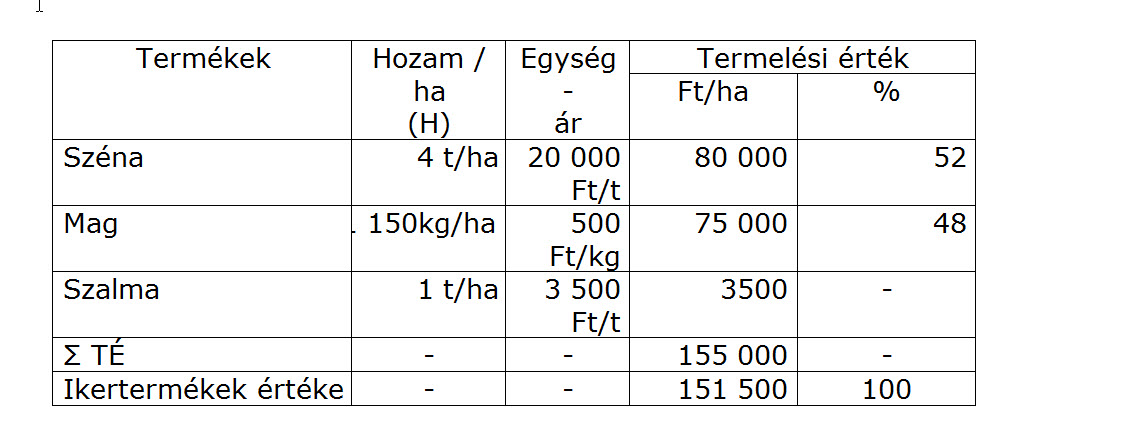
A hektáronkénti termelési költség 120.000,-Ft, ebből megtérül a szalma értéke, azaz 3.500,-Ft/ha. E kettő különbözete a nettó termelési költség összege. Azaz 116.500,-Ft/ha. Ezt az ikertermékek termelési értékének az összes termelési értékhez mért arányában (táblázat szerint) osztjuk fel, így megtudjuk az egyes termékekre eső termelési költséget:

- széna = 116 500 x 0,52 = 60.580 Ft
- mag = 116 500 x 0,48 = 55.920 Ft

Szénából azonban 4 tonna, míg magból 150 kg termett hektáronként, azaz a hektáronkénti önköltség megállapításához még tovább kell számolnunk. Azaz
- széna önköltsége= 60.580 /4 = 15.145,-Ft/t,
- mag önköltsége = 55.920/150= 372,80~ 373,-Ft/kg.

Az egyenértékszámos osztókalkulációra először nézzünk meg egy ugyancsak a mezőgazdaságból hozott példát!

Az állattenyésztéssel foglalkozó cég tehenészetében 1 év alatt 50 ezer l tejet fejtek és született 500 kg borjú. A felmerülő összes - bruttó termelési - költség (BTK) 7. 500 000 Ft a képződött trágya értéke pedig 480 ezer Ft (ez egyben a megtérülő érték is). Számítsuk ki a tej és borjú önköltségét a tapasztalati értékek alapján, ami azt jelenti jelen esetben, hogy 1 kg borjú 8 l tejjel egyenértékű.

- az ikertermékek együttes mennyisége vezértermékben (tejben) kifejezve= 500 x 8 l + 50 000 l x 1 = 54 000 l

- a vezértermék (tej) önköltsége (az összes termelési költségből levonva a megtérülő értéket):

(7.500.000-480.000)/54.000= 130,-Ft/l

- az ikertermékek önköltsége: ez egyenlő a vezértermék önköltségének és az egyenértékszámnak a szorzata, azaz

• tej = 130,- Ft/l x 1 = 130,- Ft/l
• borjú = 130,- Ft/l x 8 = 1.040 Ft/kg

Fentiekre vizsgáljunk meg még egy – ezúttal az ipari termelésből kölcsönzött – példát is!
A Trendi Termékek Kft háromféle terméket gyárt, amelyek csak méretükben különböznek. A tárgyidőszakban 4. 000 kisméretű, 7.200 közepes és 1.200 darab nagyméretű terméket gyártottak.
A befejezett termelés értéke 128.000 EFt, azaz a háromféle termék előállítása 128.000 EFt-ba került összesen.
Amennyiben az egyszerű osztókalkuláció módszerével dolgozunk (128.000 EFt/12.400 db), akkor egy olyan termék önköltségét határoznánk meg, ami valójában nem is létezik, hiszen nem vettük figyelembe a termékek méretbeli eltéréseit.

Fontos, hogy a különböző méterű termékek önköltségének megállapításához nincs szükség külön gyűjtésre, kalkulációra! A termékcsoport egy önálló kalkulációs egységként kezelhető, de találnunk kell egy megfelelő paramétert (egyenértékszámot), melynek segítségével a 128.000 EFt-ot a valóságnak leginkább megfelelő arányban szét tudjuk osztani a különböző méretű termékek között.

A három termék előállításának módja alapvetően a felhasznált alapanyag mennyiségében és a gyártás időszükségletében különbözik. Az egyszerűsítés kedvéért olyan esetet veszünk górcső alá, ahol a termékek egyféle anyagból készülnek és elkészítésük egyetlen munkaműveletből áll. A következő táblázat az egyes termékek anyag és időszükségletét mutatja:



Nem kérdéses, hogy a nagyobb anyagigényű termékre több anyagköltséget osztunk, míg az időigényesebb termékgyártáshoz több személyi jellegű költséget rendelünk. A kérdés, hogy mennyivel több költséget osszunk a nagyobb termékekre.

A válaszhoz a befejezett termelés további részletezésére van szükségünk, hiszen a közvetlen anyagköltség és a személyi jellegű költségek egyes termékekhez való hozzárendelésének eltérő alapokon kell történnie.
A befejezett termelés értékéből 48.000 EFt közvetlen anyagköltség, a többi közvetlen személyi jellegű költség (közvetlen bérköltség, személyi jellegű egyéb kifizetés és bérjárulék). Ha meghatározzuk az anyagfelhasználás és a munkaidő ráfordítás termékenkénti egymáshoz viszonyított arányát egy kiválasztott (kitüntetett) vezértermék tükrében, akkor ennek segítségével a termékenkénti önköltséget is ki tudjuk számítani.

Legyen a kiválasztott vezértermékünk a közepes méretű termék! Számítsuk ki az erőforrás felhasználások termékenkénti egymáshoz viszonyított arányát, az egyenértékszámokat!

Az egyenértékszámok az egyes normaszükségleteknek és a közepes méretű termék (vezértermék) normájának hányadosa. A nagyméretű termék anyag norma alapján meghatározott egyenértékszáma megmutatja, hogy a nagyméretű termék anyagszükséglete 5/4-szer akkora, mint a vezérterméké vagy például a kisméretű termék munkaidő norma alapján kiszámított egyenértékszáma szerint a kisméretű termék elkészítésének időszükséglete 4/5 része a vezértermék időszükségletének.

Az anyagnorma alapján képzett egyenértékszámok felhasználásával kiszámolható, hogy hány darab vezér típust tudtunk volna legyártani (termelés vezértípusban), ha az összes a tárgyidőszakban felhasznált anyagból kizárólag vezértípust – jelen esetben közepes méretű terméket - gyártunk. Az időnormák segítségével is kiszámolható egy olyan vezértípusra vonatkoztatott elméleti mennyiség, ami megmutatja, hogy mennyi közepes terméket gyárthattunk volna, ha a tárgyidőszakban teljesített munkaórák során kizárólag közepes termékeket gyártunk. Számítsuk ki a termelést vezértípusban!

Termelés vezértípusban az anyagnormák alapján meghatározott egyenértékszámok segítségével: (5/8) x 4.000 db + 1x 7.200 db + (5/4) x 1.200 db = 11.200 db
Termelés vezértípusban az időnormák alapján meghatározott egyenértékszámok segítségével:
(4/5) x 4.000 db + 1x 7.200 db + (7/5) x 1.200 db = 12.080 db

Fentiek alapján első lépésben a vezértípus önköltségét tudjuk kiszámolni, majd az egyenértékszámokkal a vezértípus önköltségéből a másik két termék önköltsége is kiszámítható. Tudjuk, hogy a közvetlen anyagköltség 48.000 EFt, a közvetlen személyi jellegű költségek 80.000 EFt (128.000 EFt – 48.000 EFt) a befejezett termelés szintjén!

Abban az esetben, amikor a termelés minden költségtétele egy vezértermékkel elemezhető (például üdítőital gyártásánál, amikor a termékek csak kiszerelésükben különböznek egymástól), vagy amikor a termék előállítási költségéből az egyik kalkulációs tételhez (közvetlen anyaköltség vagy közvetlen bérköltség) tartozó költség jelentősen nagyobb a többi költségtételhez képest, a rokontermékek önköltsége az egylépcsős egyenértékszámos osztókalkulációval meghatározható. Azonban akkor, ha különböző kalkulációs tételek szerinti költségeket eltérő egyenértékszámok jellemzik, akkor az önköltség a többlépcsős egyenértékszámos osztókalkuláció módszerével számolható.

Az egyenértékszámos osztókalkuláció lehet:
- műszaki egyenértékszámos osztókalkuláció -> a termelési folyamatban ikertermékek keletkeznek (vezértípust választanak)
- érték egyenértékszámos osztókalkuláció -> itt valamilyen érték alapján osztjuk meg a költségeket (pl. árbevétel alapján)

Az egyenértékszámos osztókalkuláció alapján történő önköltségszámítás lépései – fenti példáinkkal is szemléltetve - az alábbiak:
1. meghatározzuk az egyes termékfajták egyenértékszámait valamilyen jellemző alapján (méret, technológia, idő, felhasznált súly, eladási ár stb.); kijelöljük a „vezértípust”;
2. természetes mértékegységben meghatározott termelést az egyenértékszámmal átszámítjuk „vezértípusra”;
3. kiszámítjuk a befejezett termelés összes költségét kalkulációs tételek szerint;
4. a befejezett termelés – kalkulációs tételenként tagolt – költségeit elosztjuk a vezértípusra átszámolt termelés mennyiségével; így meghatározhatjuk a vezértípus önköltségét;
5. az egyes termékfajták önköltségét a vezértípus önköltségéből úgy határozhatjuk meg, hogy azt szorozzuk a termékfajta egyenértékszámával.

A pontos önköltségszámítás alapfeltétele a költségek pontos rögzítése, amelynek „alapkelléke” a 6-os 7-es számlaosztály számláinak vezetése. Az itt alkalmazott alszámla-bontás logikáját célszerű a 2-es számlaosztályban is követni.